Optics

Properties of Light

1. Light travels in a straight line

Light travelling in a straight line represents a ray of light. A set of straight lines represent a beam of light. The beam may be parallel, converging or diverging.

The branch of optics based on this property of light is known as Geometrical Optics

2. Light gets reflected

When the light traveling in a medium is incident on another medium, part of the light is sent back into the first medium. This is reflection. The surface separating the two media is the reflecting surface. Sometimes this surface is coated (silvered) to increase reflection. When the surface is smooth and polished it is a regular reflection giving rise to an image. Irregular reflection (scattering) occurs when the surface is not smooth.

Laws of reflection

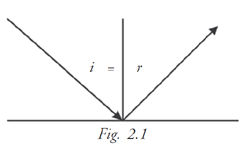
First Law: The incident ray, the reflected ray and the normal ray at the point of incidence on the reflecting surface are all in the same plane (Fig. 2.1).

Second Law: The angle of incidence is equal to the angle of reflection.

The most important application of reflection is in the plane mirror. The use of such mirrors for cosmetics is well known. The image formed on a plane mirror is virtual (not real). It is of the same size as the object and is formed as far behind the mirror as the object is in front of it. The image has left / right inversion.

Plane mirror is used in refraction cubicles to reduce the length of the cubicle to half its length. However the Snellen’s chart used with plane mirror will have objects with left right inversion so the patient sees the correct image inside the mirror.

3. Light gets refracted

When light travelling in one medium enters another there is deviation (bending) in its path. This is known as refraction which arises because of differences in the speed of light in different media.

Laws of refraction

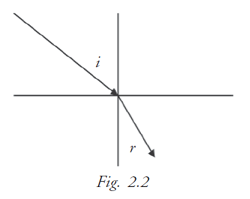
First Law: The incident ray, the reflected ray and the normal ray at the point of incidence on the refracting surface are in the same plane (Fig. 2.2).

Second Law: The ratio of the sine of the angle of incidence to the sine of angle of refraction is a constant which is known as the refractive index of the second medium with respect to the first medium. (sin i / sin r = constant).

Refractive Index

It is the ratio of speed of light in air to the speed of light in the medium. The speed of light in air is maximum (180,000 m/s). Hence the refractive index of a medium is always greater than 1.

For air n = 1, for water n = 1.33, for glass n = 1.5

Prisms and lenses used in ophthalmic practices are refraction devices.

Prism

A prism is a transparent triangular piece of glass or plastic. It has with two plane (flat) refracting sides, an apex (top) and a base (bottom) (Fig. 2.3). A ray of light incident to a prism is always bent towards the base of the prism. The image formed appears displaced towards its apex.

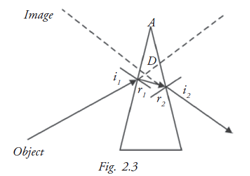
n = sin i1/sin r1 = sin i2/sin r2
Angle of deviation D = (i1+i2) – (r1+r2),
Angle of prism A = r2+r1
D = i1+i2 – A, When A is small, D = (n-1) A
For glass n = 1.5,
D = (1.5 – 1) A = A/2

The magnitude of the prism effect depends on the angle of the prism. Prisms are used to measure and also to correct muscular imbalance in patient’s eyes.

Prism diopter

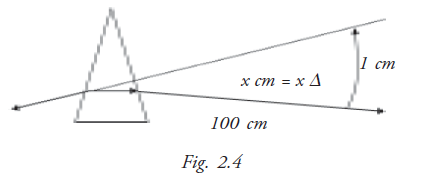
Prism power is measured by the extent of deviation produced as a light passes through it. If the displacement of the image of an object located 100 cm away from the prism is x cm when seen through the prism its power is x △(prism diopter) (Fig. 2.4).

Lens

A lens is a transparent medium bounded by two curved surfaces or one curved surface and a plane surface. Its most common application is correcting certain problems in eye sight.

Lenses can be of six different types (Fig. 2.5):

1. Biconvex lens - both sides are convex
2. Plano-convex lens - one side is plane, the other side is convex
3. Meniscus lens - convex meniscus: meniscus shaped with greater convex curvature
4. Biconcave lens - both sides are concave
5. Plano-concave lens - one side is plane and other side is concave
6. Meniscus lens - concave meniscus: meniscus with greater concave curvature

To understand the working of lenses consider two prisms placed base to base. Light rays through them coverage (come together) at some point on the other side of the prism. Similarly if two prisms are placed together apex to apex, the ray will diverge (spread apart) on the other side of the prism (Fig. 2.6).

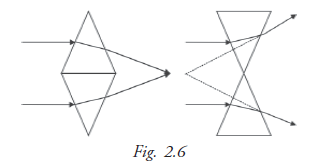
In most applications the curved surface lenses are spherical (part of a sphere) and such lenses are called spherical lenses. Lenses that converge a beam of light are known as converging, convex or positive lenses while those that diverge a beam of light are known as diverging, concave or negative lenses.

Some important terms relating to lenses

Optical centre: It is a point on a lens where a ray of light passing through it goes straight (there is no deviation). Principal axis: It is the line joining the centres of curvature of the two curved sides of the lens. In case of plano-convex or plano-concave lenses it is perpendicular to the flat surface from the centre of curvature of the other curved surface.

Focal point (Principal focus): A beam of light parallel to the principal axis of a lens after refraction converges towards a point on the principal axis (convex lens) or appears to diverge from a point on the principal axis (concave lens). This is called the focal point. There are two focal points on either side of a lens at equal distances from the optic centre.

Focal length: The distance of the focal point from the optic centre is the focal length.

Power of a lens: The reciprocal of the focal length measured in metre units is the power of the lens in diopter (D = 1/ f). It is taken as positive for convex lenses and negative for concave lenses.

Focal length	Power
1 m	1 D
2 m	(1/2) = 0.5 D
(1/2) = 0.5 m = 50 cm	2 D
3 m	(1/3) = 0.3 D
(1/3) = 0.3 m = 30 cm	3 D

Power of a lens is the sum of powers of its two surfaces.For a curved surface power P = (n – 1) / r, r being the radius of curvature of the curved surface measured in meter units.

For biconvex lens

P1 = (n – 1) / r1 ; P2 = (n - 1) / r2

Power of the lens: P = P1+P2 = {(n – 1)/r1} + {(n – 1)/r2}

P = (n - 1) (1/r1 + 1/r2)

For a plano convex lens: The plane surface has no power. For the curved surface P1 = (n - 1) /r1, the total power is P = (n - 1) (1/r1) These are known as the lens maker’s formula.

Formation of images in Lenses

Two rays are used to locate the image. A ray of light passing through the optic centre goes undeviated. A second ray of light, parallel to the principal axis, after refraction in case of convex lens converges and proceeds in the direction of the focal point on the other side. In concave lens it diverges and appears to come from the focal point on the same side.

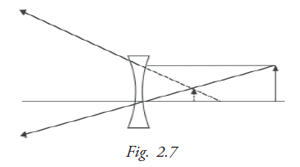
Characteristic of the image formed using a concave lens for all locations of the object

Image is formed on the same side of the lens as the object; virtual, erect and smaller in size (Fig 2.7). Concave lens is used in the correction of short sight (myopia). The eyes of a person wearing such a lens will appear smaller. This is one reason why people requiring high negative powers prefer contact lens instead of spectacle lens. Also the object seen through such a lens will appear farther than where they are actually located.

Characteristic of the image in convex lens

Case (i): Object located between the lens and principal focus (Fig. 2.8).

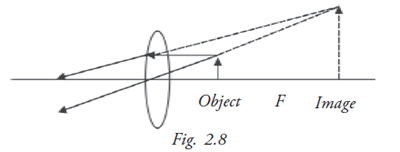
Image if formed on the same side of the lens as the object; virtual, erect and magnified. This is the principle of a simple microscope, single loop and hand -held magnifier.

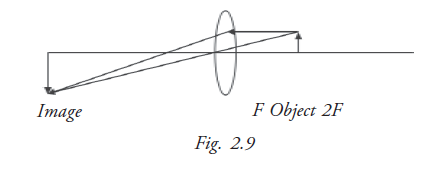
Case (ii): Object located between the principal focus (F) and twice the focal length (2F) on one side.

Image is formed beyond 2F on the other side, real, inverted and magnified (Fig. 2.9).

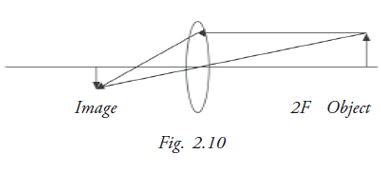
Case (iii): Object beyond 2F on one side Image is formed between F and 2F on the other side, real, inverted and smaller in size. Convex lens is used in the correction of long sight (hypermetropia / hyperopia). Objects seen through such a lens appear farther than where they actually are (Fig. 2.10).

Quick test for lenses

To distinguish between positive and negative lens look at an object at a distance from the lens and move the lens gently. If the image also moves in the same direction (with motion) it is negative lens. If the image moves in the opposite direction (against motion) it is positive lens.

Prism power in lenses: Prentice rule

A spherical lens has prism power for every point in it except for the optic center, at which the prism power is zero. In plus lenses, the prism power bends light rays toward the optic axis, and in minus lenses, it bends away from the optical axis. Prism power increases with the distance of the point from the principal axis.

Using the principle of similar triangles it can be shown that the prism power corresponding to point A at a distance ‘y’ from the principal axis is the product of the lens power and the distance y. This is Prentice rule (Fig. 2.11).

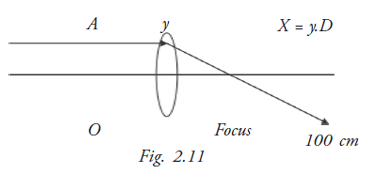
This has application in designing the reading lens part of bifocal spectacle lens for patients with presbyopia. The prism effect helps in bending the rays up to avoid looking down through the reading lens and in reducing the convergence of the eye required for looking at close objects.

Decentration

Prism effect comes into play when the distance between the optic centres of the spectacle lens is not the same as the inter pupillary distance (IPD) of the patient. Looking through such spectacle lenses will cause discomfort. This is known as decentration.

Cylindrical lenses

Lenses in which one of the curved surfaces is cylindrical are known as cylindrical lenses. They are used in correcting astigmatism (Fig. 2.12).

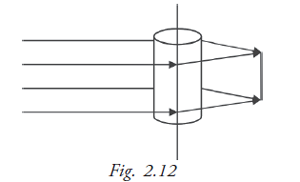
A cylinder has no curvature in a direction parallel to its axis. So it has no refractive power in that direction. It is curved in the direction perpendicular to its axis and therefore has a refractive power. The refractive power of a cylindrical surface is also P = (n – 1) / r, as in the case of spherical surface, r being the radius of curvature of the cylinder. With a cylindrical lens one gets a focal line instead of a focal point.

Astigmatism arises when one of the patient’s eyes has different powers in different axes. The extra power needs to be added or subtracted in any required axis with the help of positive or negative cylindrical lens.

Other properties of light

Some of the other properties of light are as follows. They arise because of the wave nature of light.

4. Scattering

Particles of dust, moisture, scratches on mirror, lens and prism surfaces cause scattering (irregular reflection) of light. Scattering results in loss of brightness and glare.

5. Interference

Light waves of same wavelength from different sources undergo interference. The waves reinforce (add up) producing brightness or destroy each other producing darkness. The interference effect is used in antireflection coating on the surfaces of spectacle lenses.

6. Diffraction

Because of the wave nature, light bends. This is known as diffraction. Since the wavelength of light is very small the bending is also very small and light appears to travel in straight line path. The diffraction effect limits the clarity of the final image formed in optical instruments including the eye.

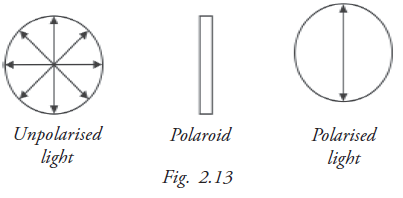
7. Polarisation

Light waves are transverse in nature. The vibrations of electric field (or magnetic field) that constitute light are at right angles to the direction of propagation of light. Ordinary light is unpolarised and has vibrations in all directions. Unpolarised light passing through a device known as Polaroid has the vibration confined to one direction. Reflection of light (unpolarised) from some surfaces also gives rise to polarised light (Fig. 2.13).

When polarised light is viewed through a polaroid there is variation in the brightness of light seen through it depending on its orientation. The light is even cut off in two orientations. This property of Polaroid to cut out strongly polarised reflected light is used in special sun glasses known as Polaroid glasses.

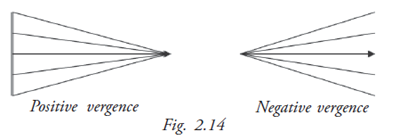
Vergence

This is a useful concept used by optometrists in their calculations (Fig. 2.14).

A parallel beam of light neither converges nor diverges. Its vergence is defined as zero.

A converging beam of light has positive vergence while a diverging beam has negative vergence. The vergence of a beam is measured in dioptre units. The vergence of a beam at a location is the reciprocal of the distance of the location in meter units from the point where the beam converges or appears to diverge.

A positive lens having a power + D introduces a positive vergence of D to a parallel beam of light while a negative lens of power – D introduces a negative vergence of D to a parallel beam of light.